	AES	DES
密钥长度	128位、192位、256位(可变的)	56位(固定的)
运算对象	面向字节	面向比特
加解密运算	不一样，因而加密器不能同时用作解密器	无AES的限制

3.SM4密码算法

密码算法结构

四、序列密码（流密码）

算法举例： RC4、A5

1.线性反馈移位寄存器

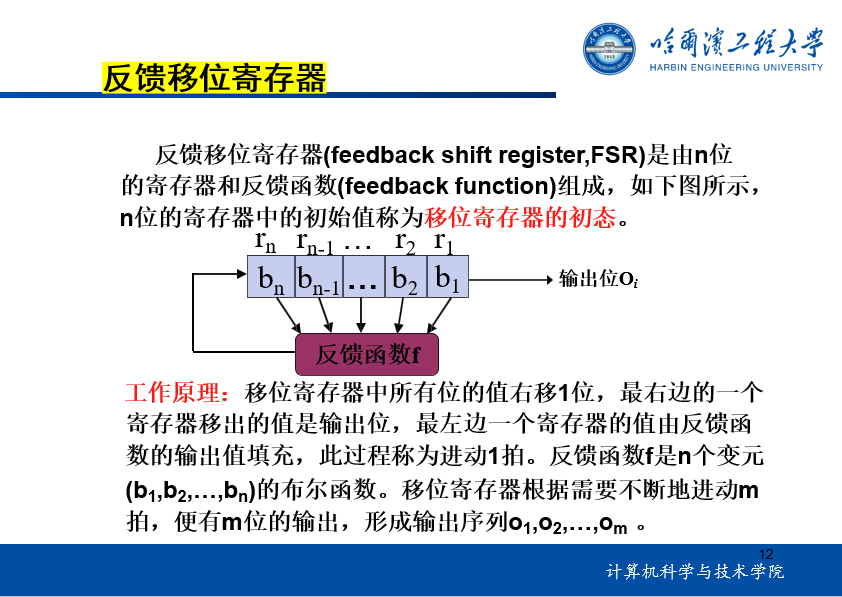
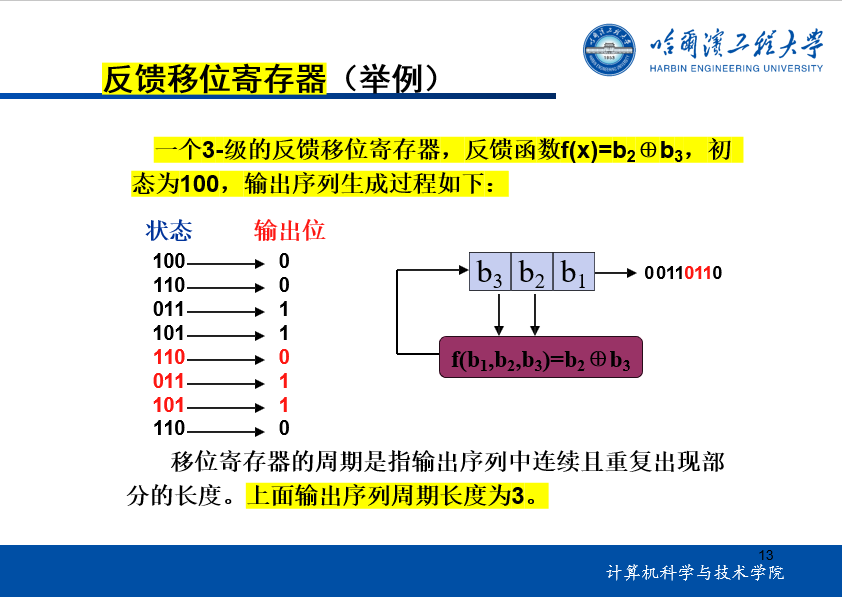
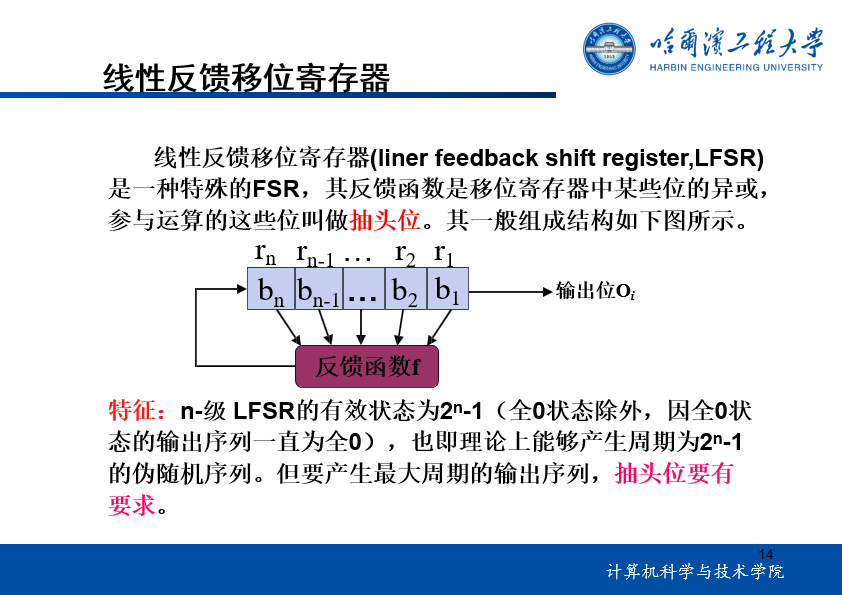
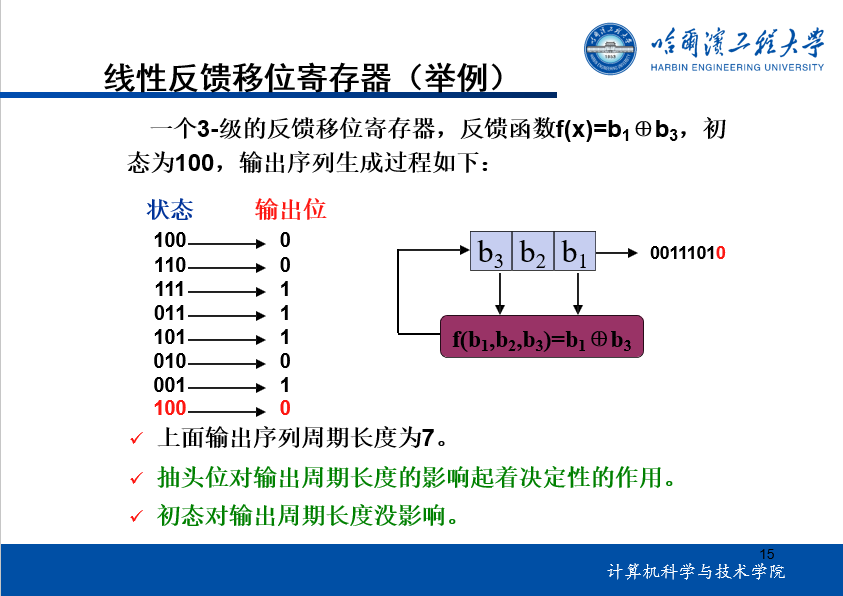
2.非线性序列

（选择填空）

Geffe序列生成器
J-K触发器
Pless生成器
门限发生器

五、密码学数论基础

1.欧拉定理

欧拉函数
设 $m$ 是一个正整数，则 $m$ 个整数 $0,1,...,m-1$ 中与 $m$ 互素的整数的个数，记为 $\phi(m)$ ,称为欧拉函数。
当 $m$ 为素数时， $\phi(m)=m-1$ ；当 $m$ 为合数时， $\phi(m)<m-1$ 。
费马小定理
设 $m$ 是素数， $a$ 是任意整数，且 $(a,m)=1$ ，则有 $a^{m-1}\equiv 1(mod\ m)$ 。
欧拉定理
设 $m$ 是大于1的整数， $a$ 是与 $m$ 互素的整数，则有 $a^{\phi(m)}\equiv 1(mod\ m)$ 。

2.模重复平方计算法

计算 $b^n(\ mod\ m)$ ，其中 $m$ 和 $n$ 都是大整数。

①将n写成二进制形式

$n$ 写成二进制形式： $n=n_0+n_1 2+n_2 2^2+...+n_{k-1} 2^{k-1}$

②计算

$a=1$

\begin{cases} a_0 = a·b^{n_0}(\ mod\ m),\ b_1=b^2(\ mod\ m)\\ a_1 = a_0·b_1^{n_1}(\ mod\ m),\ b_2=b_1^2(\ mod\ m)\\ \cdots\\ a_{k-1} = a_{k-2}·b_{k-2}^{n_{k-1}}(\ mod\ m) \end{cases}

最终得到 $a_{k-1}$ ,也就是结果： $b^n(\ mod\ m)$

3.☆中国剩余定理(CRT)(一次同余式组)☆

设 $m_1,m_2,...,m_k$ 是两两互素的正整数， $a_1,a_2,...,a_k$ 是任意整数，则同余式组

\begin{cases} x\equiv a_1(\ mod\ m_1)\\ x\equiv a_2(\ mod\ m_2)\\ \cdots\\ x\equiv a_k(\ mod\ m_k) \end{cases}

求解x的步骤：

1.计算 $m=m_1m_2...m_k$
2.计算 $M_i=m/m_i(i=1,2,...,k)$
3.计算 $M_i$ 在模 $m_i$ 意义下的逆元 $M_i^{-1}$
4.计算 $x=\sum_{i=1}^{k}a_iM_iM_i^{-1}(\ mod\ m)$

4. 整数的原根

设 $m > 1$ 是整数， $a$ 是与 $m$ 互素的正整数，则使得

a^e \equiv 1 (\ mod\ m)

的最小正整数 $e$ 称为 $a$ 对模 $m$ 的指数（或阶），记作 $\text{ord}_m(a)$ 。如果 $a$ 对模 $m$ 的指数是 $\phi(m)$ ，则称 $a$ 为模 $m$ 的原根（或本原元）。

设 $m >1$ 是整数， $a$ 是与 $m$ 互素的整数，则整数 $d$ 使得 $ad \equiv 1 (\ mod\ m)$ 成立的充要条件是 $\text{ord}_m(a) | d$ 。

推论1 设 $m > 1$ 是整数， $a$ 是与 $m$ 互素的整数，则 $\text{ord}_m(a) | \phi(m)$ 。

举例：5 模17的指数， $\text{ord}_{17}(5) = 16 = \phi(17)$ ，5是模17的原根。

六、散列函数和消息认证

1.MD5算法

1.1 消息填充

1.2 附加消息长度

1.3 初始化链接向量

1.4 处理消息分组、输出结果

七、公钥密码

对称密码体制的缺陷、要求：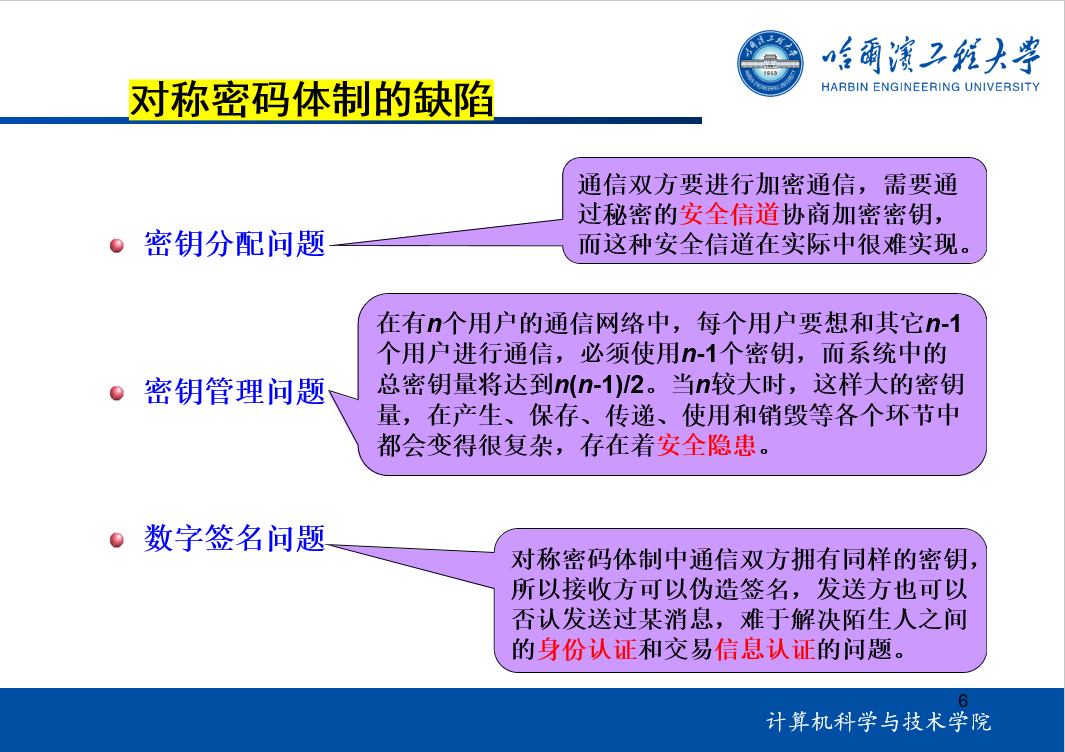

常见算法：

背包问题（NP问题、背包算法）
基于大整数素因子分解问题(RSA)
基于有限域乘法群上的离散对数问题(ElGamal)
椭圆曲线的离散对数问题(ECC)
基于身份、属性的密码体制(IBE、ABE)

1.背包算法

2.RSA算法

2.1 密钥对生成算法

3.ElGamal算法

4.RSA算法的安全性

八、数字签名

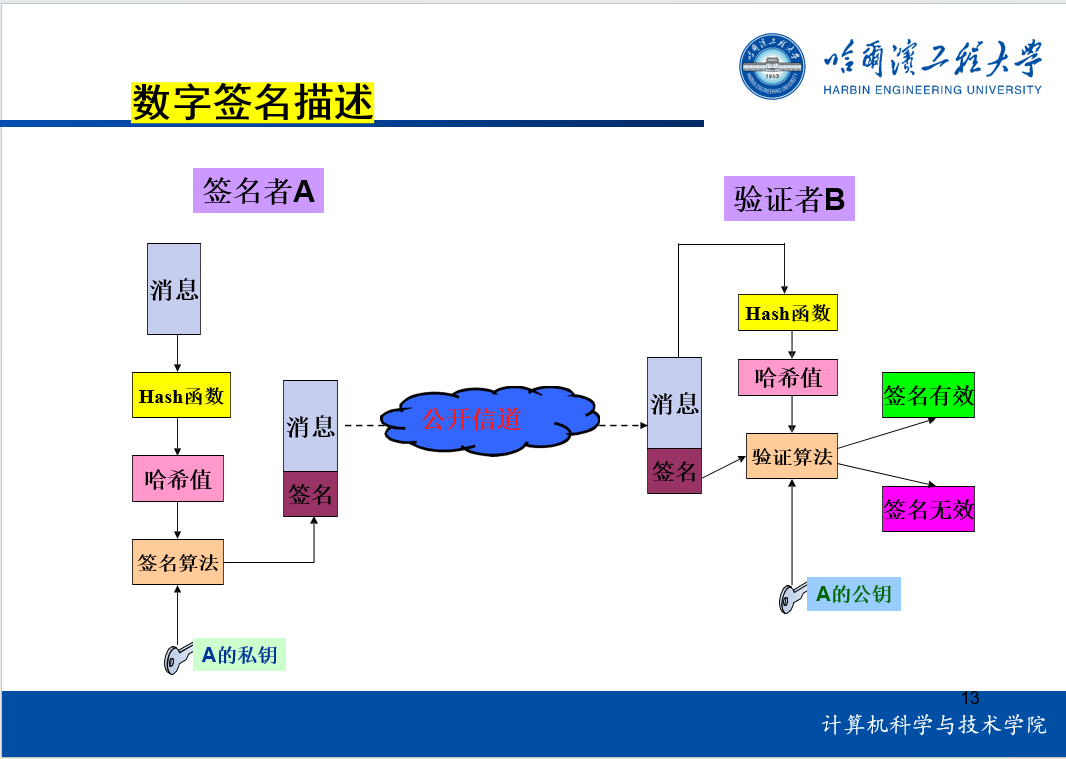
九、密钥管理

Easy

参考

https://osdoc.net/md/28/
https://chenyangwang.gitbook.io/mathematical-base-for-information-safety
https://oi-wiki.org/math/number-theory/crt/
http://www.uinio.com/Math/LaTex/

贡献者

only9464

变更历史

最后更新于: 查看全部变更历史

8a568-
Add Ubuntu
于 2024/11/29
4b6e2-
Update
于 2024/11/27
f92d1-
Update 现代密码学 & Add GoogleAnalytics
于 2024/11/27
5fbfc-
Update
于 2024/11/26
f8912-
Update
于 2024/11/25
27faa-
Update 现代密码学
于 2024/11/25